[Python] 힙 자료구조 / 힙큐(heapq) / 파이썬에서 heapq 모듈 사용하기
힙은 특정한 규칙을 가지는 트리로, 최댓값과 최솟값을 찾는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한다.
힙 property : A가 B의 부모노드이면 A의 키값과 B의 키값 사이에는 대소 관계가 성립한다
- 최소 힙: 부모 노드의 키값이 자식 노드의 키값보다 항상 작은 힙
- 최대 힙: 부모 노드의 키값이 자식 노드의 키값보다 항상 큰 힙
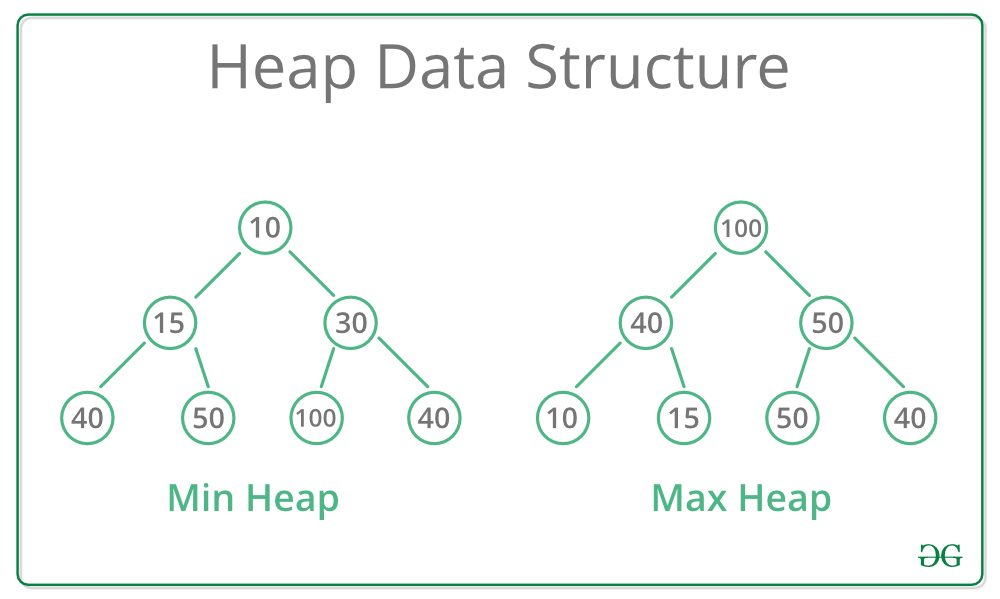
이러한 속성으로 인해 힙에서는 가장 낮은(혹은 높은) 우선순위를 가지는 노드가 항상 루트에 오게 되고 이를 이용해 우선순위 큐와 같은 추상적 자료형을 구현할 수 있다.
이때 키값의 대소 관계는 부모/자식 간에만 성립하고, 형제노드 사이에는 대소 관계가 정해지지 않는다.
파이썬 힙 자료구조
파이썬 heapq 모듈은 heapq (priority queue) 알고리즘을 제공한다.
모든 부모 노드는 그의 자식 노드보다 값이 작거나 큰 이진트리(binary tree) 구조인데, 내부적으로는 인덱스 0에서 시작해 k번째 원소가 항상 자식 원소들(2k+1, 2k+2) 보다 작거나 같은 최소 힙의 형태로 정렬된다.
heapq는 내장 모듈로 별도의 설치 작업 없이 바로 사용할 수 있다.
힙 함수 활용하기
- heapq.heappush(heap, item) : item을 heap에 추가
- heapq.heappop(heap) : heap에서 가장 작은 원소를 pop & 리턴. 비어 있는 경우 IndexError가 호출됨.
- heapq.heapify(x) : 리스트 x를 즉각적으로 heap으로 변환함 (in linear time, O(N) )
힙 생성 & 원소 추가
heapq 모듈은 리스트를 최소 힙처럼 다룰 수 있도록 하기 때문에, 빈 리스트를 생성한 후 heapq의 함수를 호출할 때마다 리스트를 인자에 넘겨야 한다.
아래 코드는 heap이라는 빈 리스트를 생성하고 50, 10, 20을 각각 추가하는 예시이다.
import heapq
heap = []
heapq.heappush(heap, 50)
heapq.heappush(heap, 10)
heapq.heappush(heap, 20)
print(heap)

이미 생성해둔 리스트가 있다면 heapify 함수를 통해 즉각적으로 힙 자료형으로 변환할 수 있다.
heap2 = [50 ,10, 20]
heapq.heapify(heap2)
print(heap2)

힙에서 원소 삭제
heappop 함수는 가장 작은 원소를 힙에서 제거함과 동시에 그를 결괏값으로 리턴한다.
result = heapq.heappop(heap)
print(result)
print(heap)

위의 예제의 경우 heap에서 가장 작은 원소인 10이 결과로 리턴되었고, 힙에서는 제거된 것을 볼 수 있다.
원소를 삭제하지 않고 가져오고 싶으면 [0] 인덱싱을 통해 접근하면 된다.
result2 = heap[0]
print(result2)
print(heap)

위의 예제에서 힙에서 가장 작은 원소인 20을 가져오고난 후에도 heap은 유지되는 것을 확인할 수 있다.
최대 힙 만들기
파이썬의 heapq 모듈은 최소 힙으로 구현되어 있기 때문에 최대 힙 구현을 위해서는 트릭이 필요하다.
IDEA: y = -x 변환을 하면 최솟값 정렬이 최댓값 정렬로 바뀐다.
힙에 원소를 추가할 때 (-item, item)의 튜플 형태로 넣어주면 튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 된다. 이때 원소 값의 부호를 바꿨기 때문에, 최소 힙으로 구현된 heapq 모듈을 최대 힙 구현에 활용하게 되는 것이다.
아래의 예시는 리스트 heap_items에 있는 원소들을 max_heap이라는 최대 힙 자료구조로 만드는 코드이다.
heap_items = [1,3,5,7,9]
max_heap = []
for item in heap_items:
heapq.heappush(max_heap, (-item, item))
print(max_heap)

heappush 함수를 통해 item을 힙에 push 할 때 (-item, item)의 튜플의 형태로 넣은 것을 확인할 수 있다.
그 결과 heappop을 사용하게 되면 힙에 있는 최댓값이 반환되는 것을 확인할 수 있다. 이때 실제 원소 값은 튜플의 두 번째 자리에 저장되어 있으므로 [1] 인덱싱을 통해 접근하면 된다.
max_item = heapq.heappop(max_heap)[1]
print(max_item)

[예제] 주어진 리스트의 모든 값이 T 이상이 될 때까지 최솟값 두 개를 합치기
N개의 비커에 액체가 담겨 있다. 모든 비커에 있는 액체의 양이 T 이상이 될 때까지 액체가 가장 적게 담긴 두 비커의 액체를 합쳐가려 한다. 각각의 비커에 담겨있는 액체의 양을 표기한 리스트 L과 기준 T가 주어질 때, 모든 비커의 양이 T 이상이 될 때까지 필요한 작업 횟수를 리턴하는 함수를 구현해보자. (구현할 수 없는 경우 -1을 리턴)
Example:

Solution: heapify, heappush, heappop 활용
import heapq
def my_heap_example(L, T):
""" 주어진 비커의 리스트를 힙 구조로 변환 """
heapq.heapify(L)
result = 0
while len(L) >= 2 : #IndexError 방지
""" 힙에서 최솟값을 가져옴 """
min_ = heapq.heappop(L)
if min_ >= T: # 액체의 최솟값이 T보다 크다는 조건 만족(종료)
print("-"*40, "\nresult:", result)
return result
else: # 두 번째로 작은 값 가져와서 합친 값을 힙에 삽입
min_2 = heapq.heappop(L)
heapq.heappush(L, min_ + min_2)
result += 1
print("step{}: [{},{}] 합칩".format(result, min_ , min_2))
print(" →", L)
if L[0] > T:
print("-"*40, "\nresult:", result)
return result
else:
print("-"*40, "\nMission Failed")
return -1
Result 1:

Result 2: 모든 비커를 합쳐도 기준값을 넘지 못해 -1을 반환하는 케이스

https://docs.python.org/2/library/heapq.html
8.4. heapq — Heap queue algorithm — Python 2.7.17 documentation
8.4. heapq — Heap queue algorithm Source code: Lib/heapq.py This module provides an implementation of the heap queue algorithm, also known as the priority queue algorithm. Heaps are binary trees for which every parent node has a value less than or equal to
docs.python.org
