** Previous **
2020/08/16 - [AI] - Active Learning - ① 액티브 러닝이란 무엇인가
Active Learning - ① 액티브 러닝이란 무엇인가
액티브 러닝이란? 전통적으로 기계학습(Passive Machine Learning)은 라벨링되지 않은 데이터에 대해 사람이 라벨을 부여하면 이를 기계가 학습하는 방식으로 이루어졌다. 이 방식에서는 학습 데이터 �
littlefoxdiary.tistory.com
액티브러닝의 핵심은 러너가 아직 라벨링 되지 않은 데이터 중 가장 정보 혹은 효용이 높은 인스턴스를 쿼리하는 데에 있다. 이렇게 라벨링이 필요한 데이터를 선택하는 전략을 쿼리 전략(query strategy)이라고 부른다. 쿼리 전략 중 한 가지가 이전 포스팅에서 소개한 Uncertainty Sampling이다. 불확실성에 기반한 전략으로 LC, Margin Sampling, Entropy Sampling 전략을 소개하였는데, 이들은 공통적으로 모델이 인스턴트에 대해 예측한 확률 값에 기반하여 라벨링 할 데이터를 선택한다.
본 포스팅에서는 Uncertainty Sampling 이외에 쿼리 전략으로 선택할 수 있는 다섯 가지 전략을 추가로 소개한다.
1. Query-by Committee(QBC 알고리즘)
QBC 접근법에서는 (C)개의 모델로 구성된 위원회 집단을 포함한다. 이 모델들은 모두 현재 라벨링 된 데이터셋 L에 대해 학습한 모델이지만, 서로 상충되는 가설을 다룬다. 각각의 위원회 구성원은 어떤 쿼리 후보를 질의할지에 대해 투표를 진행하고, 각각의 모델이 가장 많은 의견상충을 보인 쿼리가 가장 정보가 많은 쿼리라고 가정한다.
QBC 프레임워크는 현재 라벨링된 데이터셋 L과 일관되는 가설의 집합인 version space를 최소화한다는 전재를 가지고 있다. 아래 그림 6은 각기 다른 이진 분류 태스크에서 (a)선형 함수 (B) 박스 분류기에 대한 version space의 개념을 나타낸다. 머신러닝의 목표가 version space 안에서 최고의 모델을 찾는 데에 있다면, 액티브 러닝의 목표는 가능한 한 적은 인스턴스만으로 이 공간의 크기를 최대한 제한함으로써 탐색이 더 정교해지도록 하는 데에 있다. QBC는 인풋 공간에서 모순이 있는 부분을 쿼리함으로써 이러한 목표를 달성하고자 한다.

QBC 알고리즘이 작동하기 위해서는
1. version space의 다양한 영역(region)들을 표현하는 모델의 위원회를 구성할 수 있어야 하고
2. 위원회의 구성원간의 "부동의"를 측정할 수 있어야 한다.
기존 연구에서는 현재 데이터 집합 L에 대한 두 개의 랜덤한 가설을 샘플링하는 방식으로 진행했다. 예를 들어 생성 모델의 경우, 어떤 사후 분포 P(θ|L)을 가지는 모델들로부터 랜덤 샘플링하는 방법을 사용할 수 있다. 분류 모델의 경우 query-by-boosting 이나 query-by-bagging 등의 방법을 사용할 수 있다.
구성원 간의 의견 차이를 측정하는 척도는 크게 다음의 두 가지 방법이 있다.
i. vote entropy: 엔트로피 기반의 uncertainly sampling를 QBC로 일반화한 것으로 생각할 수 있음.
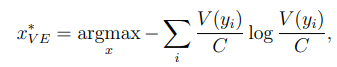
▲ y_i: 모든 가능한 라벨, V(y_i): 위원회 구성원들이 예측치에 따라 한 '투표'의 개수, C: 위원회 구성원 수
ii. 평균 Kullback-Leibler(KL) divergence 기반: 가장 정보량이 높은 쿼리는 라벨 분포 간의 평균적인 차이가 가장 큰 쿼리이다.
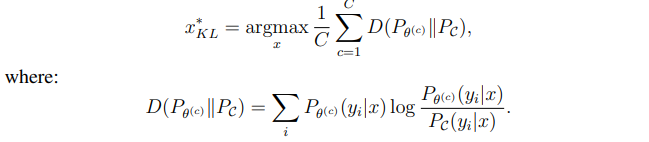
이 식에서는 사후분포에 대한 추정을 위원회 구성원들이 "hard"한 투표를 한다고 가정하고 쓴 것이지만, 각 구성원의 정확도에 따라 가중치를 주는 "soft"한 방식으로의 변경도 가능하다.
2. Expected Model Change
실제 라벨을 알았을 때 현재 모델을 가장 크게 변화시키는 인스턴스를 쿼리 하는 전략이다. Expected Gradient Length(EGL) 전략이 대표적이다. 이론적으로 이 전략은 그라디언트 기반의 학습을 하는 모든 학습 문제에 적용할 수 있다. 모델에 가해지는 변화는 학습 그라디언트의 길이(파라미터 값을 다시 측정하기 위해 사용하는 벡터)로 측정할 수 있고, 따라서 러너는 학습 셋에 추가되었을 때 학습 그라디언트가 가장 큰 인스턴스를 선택한다. 학습 그라디언트를 측정할 때, 실제 라벨 y를 알지 못하기 때문에 가능한 모든 라벨에 대해 기댓값을 취하는 전략을 취한다.

이때 쿼리시에는 , ||∇l_θ(L)||가 0 가까이 있어야 한다. l은 이전 학습 시에 수렴했기 때문이다. 따라서 위 식에서

으로 근사해서 계산할 수 있다.
이 방법에서는 쿼리의 실제 라벨과는 상관 없이 모델에 가장 많은 영향을 줄 수 있는 인스턴스를 선호한다. 실험적으로 이 방법이 잘 작동한다는 것이 증명되었지만, feature space와 라벨링 셋이 많아지면 계산 비용이 매우 비싸진다. 또한, feature을 적절히 스케일링하지 않으면, feature value가 유난히 크다는 이유만으로 인스턴스의 중요도가 과평가되는 등, 방향성을 잃을 수 있다. 실제로는 이러한 문제가 심각하지는 않고, 혹시 문제가 되더라도 파라미터 정규화로 어느 정도 방지할 수 있다고 한다.
3. Expected Error Reduction
인스턴스가 추가되었을 때, 일반화 에러(generalization error)를 최소화하도록 노력하자는 아이디어이다. 이 접근법에서는 현재의 학습 데이터 + 라벨링되지 않은 인스턴스에 대해 모델을 학습했을 때 기대되는 미래의 error를 추정한다. 그리고 risk라고 부르는 expedted future error를 최소화하는 인스턴스를 쿼리한다. 이 방법의 예시로는 기대 0/1-loss를 최소화하는 방법이 있다.

여기서 $\theta^{+<x, y_i>}$는 학습 튜플 <x, y_i>를 학습 셋 L에 추가하고 재학습한 새로운 모델을 나타낸다. 이 셋팅에서 목표는 잘못된 예측치의 기대 개수를 줄이는 것이다. 혹은 기대되는 log-loss를 최소화하는 것으로 생각할 수 있다.

위의 식은 U에 대한 기대 엔트로피를 줄이는 것과 같다고 해석할 수 있다. 혹은, 쿼리 x에 대해 기대되는 information gain을 최대화 한다, x와 U에 대한 아웃풋 변수의 mutual information을 최대화한다 라고 해석할 수도 있다.
그러나 이 방법은 계산 비용이 지나치게 커서, 이진 분류 이상의 태스크를 수행하기에는 실용적이지 않은 것으로 나타났다.
4. Variance Reduction
Loss 함수의 기대값을 최소화하는 것은 계산적으로 비싸고, 일반적으로 closed-form으로 나타낼 수 없다. 하지만 일반화 에러를 간접적으로 줄일 수가 있는데, output variance를 최소화하는 방식을 사용하는 것이다. 이 방법은 심지어 closed-form 해법을 가질 때도 있다. 하지만 이 방법에서도 계산 복잡도가 높다는 단점이 있다고 한다.
5. Density-Weighted Methods
에러를 추정하게나 variance를 줄이는 프레임워크의 핵심 아이디어는 각각의 인스턴스가 아닌 전체 인풋 공간을 고려하자는 것이다. 이러한 아이디어로 인해, 이 쿼리 전략들은 uncertainty 기반의 샘플링과 같은 단순한 전략에 비해 아웃라이어를 쿼리하게될 경향성이 적다는 강점이 있다.
아래 그림은 이진 분류 문제에서 uncertainty sampling을 사용할 때 나타날 수 있는 그림을 나타낸 것이다. 색깔이 칠해진 데이터 포인트는 각각의 라벨로 라벨링이 완료된 데이터고, 속이 비어있는 원은 라벨링 되지 않은 데이터를 나타낸다. 데이터 A는 현재의 분류 바운더리에 위치해 있기 때문에 가장 불확실성이 높고, uncertainty 전략 하에서는 이 인스턴스를 쿼리 하게 될 것이다. 하지만 이 데이터는, 나머지 데이터와는 상당히 동떨어져있다. 따라서, 해당 인스턴스의 실제 라벨을 알아낸다고 해도 전체 데이터에 대해 분류 정확도가 높아지지 않을 수도 있다.

라벨링 되지 않은 전체 pool을 사용해서 미래의 error나 아웃풋 variance를 추정하고, 이 정보를 활용하게 되면 위와 같은 상황에서 아웃라이어를 쿼리 하게 되는 문제를 피할 수 있다. 하지만 아웃라이어를 쿼리하는 문제를 방지하는 다른 방법도 존재하는데, 바로 쿼리 선택 단계에 인풋 분포를 명시적으로 모델링하는 방법이다.
Information density framework는 density-weighting 전략의 대표적인 예시이다. "정보량이 많은 인스턴스는 모델 입장에서 불확실할 뿐만 아니라 인풋 분포를 잘 나타낸다 (인풋 공간에서 밀집된 곳에 위치한다)"라는 아이디어에 기반한다. 따라서, 다음의 식을 따르는 인스턴스를 쿼리하고자 한다.

여기서 φ_A(x)는 어떤 "base" 쿼리 전략(불확실성/QBC 접근법 등..) A에 따른 x의 정보 가치를 나타낸다. 위 식에서 두 번째 항은 x의 정보량(informativeness)을 인풋 분포(U)에 따른 다른 인스턴스와의 평균적인 유사성에 근거해 계산한다. 여기서 베타 항은 이 density에 대한 항의 중요도를 나타내는 파라미터이다.
만약 density들을 미리 계산해놓고 캐싱해둘 수 있다면, 다음 쿼리를 선택하는 데에 필요한 계산 시간은 uncertainty sampling에 비해 크게 증가하지 않는다는 연구 결과도 있다. 따라서 이 전략은 real-time으로 액티브 러닝을 수행하는 데에 유용하게 사용할 수 있다.
** 참고논문: http://burrsettles.com/pub/settles.activelearning.pdf

'AI > Algorithm&Models' 카테고리의 다른 글
| [논문리뷰] Small Language Models Are Also Few-Shot Learners (2) | 2020.10.09 |
|---|---|
| AI는 딥러닝을 넘어 "깊은 이해"의 단계로 넘어가야 한다 (0) | 2020.09.12 |
| Active Learning - ① 액티브 러닝이란 무엇인가 (0) | 2020.08.16 |
| [OpenAI] Image GPT - 이미지 분야에 트랜스포머 활용하기 (0) | 2020.08.10 |
| Transformer 위치 인코딩이 가지는 성질 & 의미 (0) | 2020.07.29 |