해싱 (Hashing)
키 값에 직접적인 산술 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산해 항목에 접근하는 방법.
충분히 큰 공간을 할당한 다음 해시 함수를 이용해 고유 색인을 생성하고, 색인에 맞는 위치에 데이터를 저장하는 것이 특징이다.
- 해시함수 : 임의의 길이를 갖는 임의의 데이터를 고정된 길이의 데이터로 매핑하는 함수
- 해시 테이블 : 키 값의 연산에 의해 직접 접근이 가능한 구조
- 해싱 : 해시 테이블을 이용해 탐색하는 것
해싱에서는 자료를 저장하는 데 배열을 사용한다. 배열은 항목이 저장된 주소를 알고 있을 경우 빠르게 자료를 삽입하고 꺼내올 수 있기 때문이다. 배열에서의 삽입/ 접근에 대한 시간 복잡도는 O(1) 이다. 따라서 데이터를 색인으로 매핑하는 함수만 정의한다면, 이론적으로 O(1) 의 복잡도로 데이터를 효율적으로 탐색할 수 있다. 참고로 일반적인 탐색 방법은 정렬이 되어 있지 않을 경우 O(n), 정렬되어 있는 경우 O(log_2 n)의 복잡도를 갖는다.
해싱 알고리즘
- 해시 함수는 탐색할 키를 입력받아 해시 주소(hash address) 생성
- 생성된 해시 주소는 해시 테이블의 인덱스에 해당함
- 인덱스를 이용해 배열에 접근하여 해당하는 위치에 자료를 저장하거나 배열로부터 자료를 꺼내올 수 있음
예를 들어 H(x) = x modulo 1000, 즉 x를 1000으로 나눈 나머지를 해시 함수로 사용하는 경우를 생각해보자.
자연수 key로 3401이 들어오면 해시 함수는 키를 즉각적으로 변환하여 해시 주소 1을 생성한다.
그러면 해시 테이블의 1번 인덱스에 해당하는 버킷을 탐색하여 자료를 가져오게 된다.
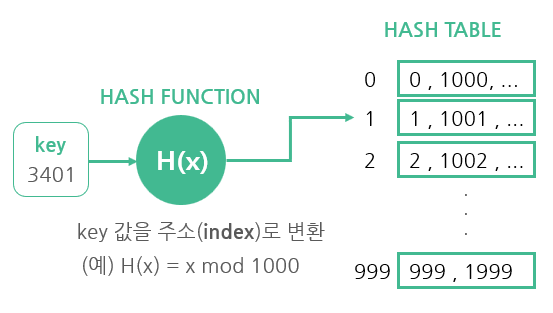
그런데 위의 해시 함수를 보면 다양한 키들이 같은 해시 주소로 변환될 수 있다. 예를 들어 (0, 1000, 2000, ... )은 모두 인덱스 0번에 해당한다. 이렇게 서로 다른 키들이 하나의 해시 주소에 매핑되는 것을 충돌이라고 부른다. 각각의 고유값을 주소로 활용(예. H(x)=x)하지 않는 이상, 지금까지 만들어진 어떤 함수도 충돌을 피할 수는 없다(비둘기집의 원리). 하지만 충돌이 많아지게 되면 같은 버킷 내 데이터들을 순차적으로 한 번 더 탐색하는 과정에서 성능이 저하된다. 특히 충돌이 한 군데에서만 편향적으로 심하게 발생하여 탐색 효율이 떨어지는 현상을 군집화라고 한다. 이러한 군집화 혹은 심한 충돌을 피하기 위해 좋은 해시함수를 설계해야 한다.
라빈 카프 알고리즘 (a.k.a Rabin-Karp Fingerprinting)
라빈 카프 알고리즘은 긴 문자열을 해싱하는데에 사용하는 대표적인 알고리즘이다.
특히 아주 긴 문자열을 순차적으로 들여다보며 패턴 일치 여부를 탐색하는 경우 아주 유용하다.
주어진 문자열에서 abcdea라는 패턴을 찾아내는 경우를 생각해보자.
길이 N인 문자열에서 길이 M인 패턴을 찾아내기 위해 단순 무식한 방법으로 패턴 비교를 하면 O(NM)의 시간이 걸린다.

이번에는 해시 함수를 이용해서 문자열을 매칭하는 방법을 생각해보자.
앞에서부터 패턴의 길이 M만큼에 해당하는 문자열을 가져와 임의의 해시 함수를 이용해 변환하고, 해시 주소가 패턴의 해시값과 비슷할 때만 패턴 매칭을 통해 일치 여부를 판별해보는 것이다.
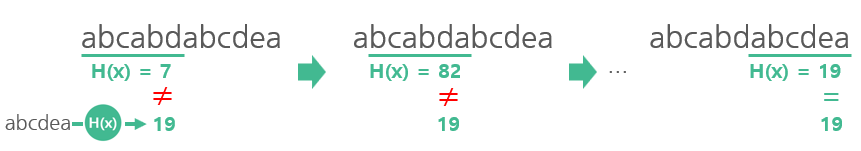
하지만 문자열을 해싱하는데에도 적어도 문자열 길이만큼의 시간이 소요된다.(O(M) )
따라서 위와 같은 방법은 그럴듯해 보이지만, 결국 각각의 위치에서 해싱을 하다 보면 시간 복잡도는 마찬가지로 O(NM) 이 된다.
그래서, 해시값을 빨리 계산하기 위해 사용하는 해시함수가 바로 Rabin fingerprint이다.
라빈 카프 알고리즘에서는 다음과 같은 식을 이용해 문자열을 변환한다. (x는 임의의 수)

이를 알고리즘적으로 풀어쓰면 다음과 같이 쓸 수 있다.
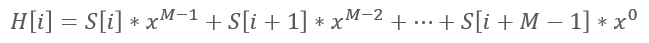
H[i]는 문자열 S에서 S[i : i+M] 부분을 해싱한 값을, S[i]는 i번째 문자열의 아스키코드를 나타낸다.
알파벳의 경우 a, b, ..., z를 아스키코드를 이용해 1, 2, ... , 26으로 인코딩할 수 있다.
x는 너무 많은 해시 충돌을 피할 수 있는 적당히 큰 수를 사용하면 된다. 예를 들어 x=10을 이용해 패턴 abcdea를 변환하면
1*10^5 + 2*10^4 + 3*10^3 + 4*10^2 + 5*10^1 + 1*10^0 = 123451이 된다.
이 알고리즘의 특별함은 i+1번째 문자열을 해싱하는 식을 풀어써보면 드러난다,
아래와 같이 i번째 문자열을 해싱하는 식을 풀어보면, i번째 문자열의 해시값을 써서 일종의 점화식 형태로 나타낼 수 있다.
이제, i+1번째 문자열의 해시값은 이전 위치의 해시값을 이용해 O(1)에 계산할 수 있는 것이다!
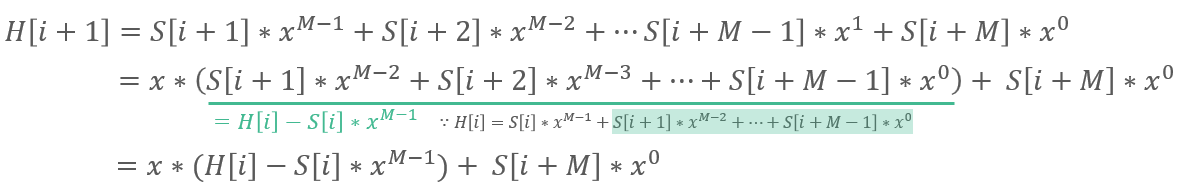
처음의 예제를 다시 살펴보면, 이전 위치의 해시값을 이용해 다음 문자열의 해시값을 빠르게 구할 수 있고, 찾으려는 문자열의 해시값과 비교해 매칭 되는 경우에만 다시 한번 단순비교 함으로써 빠르게 문자열을 찾을 수 있다!
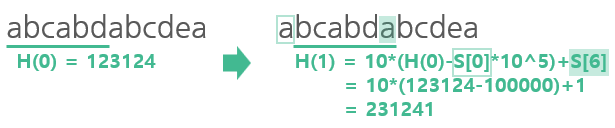
참고로 해시 함수에는 x에 대한 승수 계산이 들어가기 때문에 모듈로 연산을 취해 오버플로우를 방지해주는 것이 좋다.
모듈로 연산은 (a + b) % c = (a % c) + (b % c) 의 성질을 가지기 때문에, 위에서 해시값을 계산하는 중에 필요한 덧셈 연산을 취할 때마다 적당히 백만 ~ 십억 사이의 값으로 모듈로 연산을 취함으로써 라빈-카프 알고리즘을 안정적으로 활용할 수 있다 :)

'Others > Coding' 카테고리의 다른 글
| [TopCoder 알고리즘] 시뮬레이션 - 키위주스 (0) | 2022.03.31 |
|---|---|
| [2021 Hackathon] 2. Modeling (0) | 2021.01.31 |
| [2021 Hackathon] 1. Data Preprocessing (1) | 2021.01.29 |
| [Python] IR 검색 알고리즘 - BM25 / 엘라스틱서치 랭킹 알고리즘 / 파이썬 rank_bm25 모듈로 문서 검색 구현하기 (0) | 2020.03.01 |
| [Python] 힙 자료구조 / 힙큐(heapq) / 파이썬에서 heapq 모듈 사용하기 (4) | 2020.02.23 |