Graph Convolutional Networks (GCN) 개념 / 정리

Graph Neural Networks (GNN) 복습

- Graph란 방향성이 있거나(directed) 없는(undirected) 엣지(edge)로 연결된 노드(nodes=verticles)들의 집합

- RNN을 이용해 인접한 노드의 정보를 취합하고, 그래프 전체를 하나의 representation으로 나타낼 수 있음

- 그래프 구조의 유연성으로 인해 자연적으로 그래프 형태를 가지는 소셜 네트워크 데이터, 분자 구조 등뿐만 아니라, 기존에 다른 형태로 표현되던 이미지 데이터 등도 그래프로 나타낼 수 있음

 

참고 >> 2020/03/10 - [AI] - Graph Neural Networks (GNN) / 그래프 뉴럴 네트워크 기초 개념 정리

Graph Neural Networks (GNN) / 그래프 뉴럴 네트워크 기초 개념 정리

---

Graph Convolutional Networks (GCN)

이번에는 그래프 구조에 대해 convolution 연산을 적용하는 GCN에 대해 알아보자.

 

이미지 데이터 분석에 많이 사용되는 convolutional neural network (CNN)는 이미지를 작은 구역으로 나누어 지역적인 정보를 계속 취합하는 식으로 작동한다. 일반적으로 CNN을 사용하는 네트워크에서는 convolution 연산과 pooling 연산을 반복적으로 수행하는데, convolution은 각각의 구역으로부터 정보를 추출하는 작업을, pooling 연산은 추출된 정보 중 태스크 수행(이미지 분류 등)에 중요한 정보만을 남기는 작업이라고 생각할 수 있다.

 

<Source : https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53>

 

GCN에서도 CNN과 마찬가지로 태스크 수행에 있어 가장 중요한 정보를 그래프에서 뽑아내는 것이 목표이다. GCN은 필터를 그래프에 대해 통과시켜 그래프 내에서 중요한 노드와 엣지로부터 정보를 취합한다.

GCN Formulation

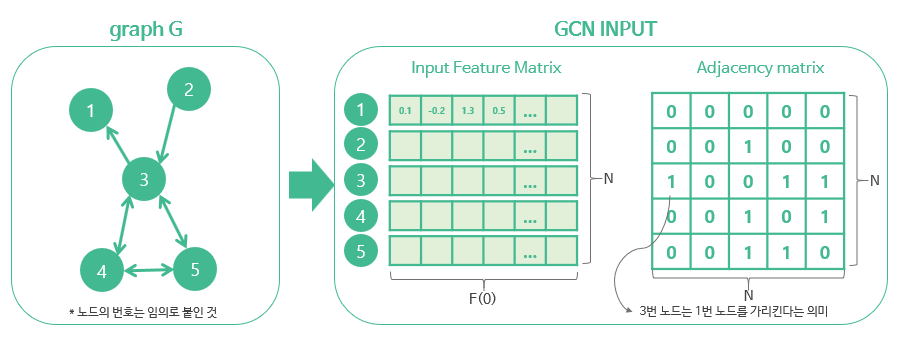
그래프 G = (V, E)가 주어질 때 GCN은 다음을 인풋으로 받는다:

- 인풋 feature 매트릭스 : 사이즈 = N x F(0)  (N: 노드 개수 F(0) 각 노드에 있는 인풋 feature 차원) 

- 그래프 구조에 대한 표현 : 사이즈 = N x N , 그래프 G의 인접성 행렬 (adjacency matrix) 등을 사용

 

 

이 때 GCN의 히든 레이어는 다음과 같이 표현할 수 있다

 

 

 

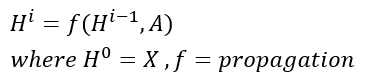
여기서 각 레이어 H^i 는 N x F(i) feature matrix를 의미한다 (각 행이 노드에 대한 representation)

각각의 레이어의 feature들은 propagation rule f에 따라 취합되어 다음 레이어로 넘어가게 된다.

이런 프레임으로 보면 다양한 GCN의 변형들은 결국 propagation rule을 어떻게 정하느냐에 따라 달라지게 된다.

 

CNN에서 첫 번째 레이어가 엣지, 색깔과 같은 기본적인 특성을 포착하고, 뒷 레이어로 갈수록 추상적인 feature를 포착하는 것처럼, GCN에서도 나중 레이어로 갈수록 그래프에서 더욱 추상적인 특성을 뽑아내게 된다. 

 

Simple Propagation Rule 

가장 간단한 룰은 다음 식을 사용하는 것이다 :

 

 

W^i 는 i번째 레이어의 weight 매트릭스로, F(i) x F(i+1) 차원을 가진다 (feature의 차원을 변화시킴)

한 레이어의 weight는 그래프에 있는 노드 전체에 대해 공유한다는 점에서 CNN의 convolution 연산과 유사하다.

 

이런 간단한 propagation rule은 다음과 같이 이해할 수 있다.

 

먼저 행렬은 결합 법칙이 성립하기 때문에 A * H^i * W^i 는 A * (H^i * W^i) 로 계산할 수 있다 (편의상 *를 행렬곱으로 표현) 

H^i * W^i 연산은 i번째 레이어에 있는 F(i) 차원의 feature을 F(i+1) 차원으로 바꾸며 정보를 추출하는 것이다.

이 연산의 결과는 아래 그림에서 하늘색 매트릭스로 표현하였다.

 

 

이제 새로 만들어진 매트릭스에 대해 인접성 행렬을 곱하면, 결과로 나오는 행렬의 (i, j)의 값은 노드 i와 연결된 모든 노드의 j번째 행렬 값의 합으로 구해진다. 즉, 각각의 노드와 연결되어 있는 노드의 정보를 모아 feature을 업데이트하는 것이다.

 

그런데 이렇게 계산할 때 문제점이 두 가지 보인다.

1. 자기 자신의 feature은 특성을 모을 때 반영되지 않는다.

    - 예를 들어 첫 번째 노드는 아무 노드도 가리키지 않고 있기 때문에, 어떠한 정보도 반영되지 않고 있다.

    - 즉, 스스로를 가리키는 self-loop을 가지고 있는 노드만이 feature을 취합할 때 자신의 정보를 반영할 수 있다.

    - 노드의 feature을 만드는 데에 있어 자신의 정보를 포함하지 않는 것은 직관적으로 생각해도 이상하다!

2. 연결이 많이 되어 있는 노드는 feature representation에서 큰 값을 가지고, 연결이 적은 노드는 값이 작아진다

    - 이로 인해 많은 노드와 연결되어 있는 3번 노드에 대한 그라디언트는 폭발하고, (exploding gradient)

    - 연결이 적은 1, 2번 노드의 경우 그라디언트가 소실될 수 있다 (vanishing gradient)

 

따라서, 다음과 같은 두 가지 트릭을 이용해 문제점을 해결한다.

1. Self-loop 포함하기

   - 각각의 노드에 대해 self loop를 주어, 인접성 행렬 A의 대각 원소는 1의 값을 가지게 한다

   - 이렇게 하면, feature을 취합할 때 항상 자신의 특성을 고려할 수 있게 된다.

2. feature representation 정규화하기

   - 노드의 연결성에 대해 계산된 feature을 정규화(normalize)함으로써 back-propagation을 안정화할 수 있다.

   - 노드의 연결성을 차원(degree)라고 부르는데, 인접 행렬 A의 차원(D)에 대한 역행렬을 곱해주면 정규화를 할 수 있다.

 

 

---

[마무리] 2D Convolution vs Graph Convolution

 

<Source: A Comprehensive Survey on Graph Neural Networks>

 

정리하자면, 이미지 2D convolution과 그래프 convolution은 모두 지역적인 정보를 취합해 feature을 고도화하는 과정이다.

둘의 차이점은

- 2D convolution은 특정 픽셀(혹은 위치)과 인접해있는 지역의 정보를 모은다

- 그래프 convolution은 노드와 연결되어 있는 노드들의 정보를 모은다

 

이 때 정보를 취합하는 방법(W matrix)은 한 레이어 안에서 모든 위치 혹은 노드에 대해 공유된다.

 

---

참고 자료:

https://arxiv.org/pdf/1901.00596.pdf

https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780

---