** 본 포스팅은 김민형 교수님 저, <수학이 필요한 순간>의 5강 내용을 바탕으로 작성하였습니다.
잘 나가는 결혼 중매 회사가 되는 법?
갑자기 궁금해져서 듀x와 가x에서 연애 테스트(?)를 해봤당. 좋아하는 색깔, 비 올 때 기분이 좋은지 등 취향에서 시작해서 나의 학력, 키, 거주지, 연봉, 직업, 나이, 성별(?) 등을 물어보았고, 원하는 상대의 연봉, 키, 학력 등도 질문지에 있었다.
아마도 중매라는 것은 후보들의 교육수준, 집안, 재력, 외모뿐만 아니라 사회문화적인 요소들을 고려해 이루어지나 보다. 이 모든 것 들을 단순화해 생각한다면 다양한 조건들이 반영된 후보들의 '선호도'에 따라 중매를 해준다고 할 수 있겠다. 마음이 있는 사람들끼리 이어준다면? 그 중매는 굉장히 성공적일 것이다.
중매인의 룰
* 본 포스팅의 내용은 드라마의 내용과는 일절 관련이 없으며 따라서 스포도 없습니다 *
사심을 담아 요즘 푹 빠져 있는 🖤이태원 클라쓰🖤의 주인공 남녀들로 예제를 만들어 보았다.
- 새로이는 수아를 이서보다 좋아한다
- 근수는 이서를 수아보다 좋아한다
- 이서는 근수를 새로이 보다 좋아한다
- 수아는 새로이를 근수보다 좋아한다
이런 상황을 선호도표로 나타내면 아래 그림과 같다.

이런 상황에서 중매인은 간단하게 새로이와 수아, 근수와 이서를 이어주면 된다.
서로 가장 '선호하는' 후보와 매칭이 되었으니 불만이 없을 것 같다.
하지만 현실 상황은 늘 그렇듯 이렇게 아름답지가 않다. 다음과 같은 상황을 생각해보자.

인기남과 인기녀가 있는 상황이다. 모든 남자가 이서를 마음에 두고 있고, 모든 여자가 새로이를 좋아한다. (나도 그렇다)
이제 어떻게 짝을 지어줘야 할까?
새로이♥수아, 근수♥이서 커플을 만들어준다면?
두 커플 모두 적어도 한 사람(인기남과 맺어진 수아, 인기녀와 맺어진 근수)은 행복한 상황이 된다.
하지만 만족하지 못 하고 있던 새로이가 마찬가지로 만족하지 못하고 있던 이서와 바람을 피우는(?) 상황이 벌어질 수 있다.
이렇게 선호도를 엇갈려서 맞추게 되면 두 커플이 모두 깨질 가능성이 높다.
중매인으로써 맺어주었던 커플에 불화가 생기는 것은 평판에 큰 악영향이 된다.
그래서 중매인은 다음과 같은 원칙에 따라 커플을 맺어주기로 한다
"안정성의 원리 : 모든 커플이 맺어지고 나면, 깨질 일이 없는 안정적인 상태로 만들자"
예를 들어 위 상황에서 인기 남녀인 새로이♥이서, 그리고 남은 근수♥수아를 맺어주게 되면, 서로를 가장 선호하는 새로이-이서 커플은 깨질 일이 없다. 근수-수아 커플은 비록 서로 가장 선호하던 상대는 아니지만, 어쩔 수 없기 때문에 깨지지 않는다. 이렇게 더 선호하는 상대로 갈아탈 수 있는 여지가 없는 상태를 안정적인 상황이라고 표명한다.
그렇다면 성사해 주어야 하는 회원이 만 명이 넘어가는 대규모 결혼정보회사에서도 이런 안정성의 원리에 따른 중매의 '답', 즉 안정적인 해를 구할 수 있을까?
이 질문에 대한 답은 Yes, 이에 대한 증명이 담겨 있는 알고리즘이 바로 게일-섀플리 알고리즘이다.
게일-섀플리 알고리즘
게일-섀플리 알고리즘은 서로에 대한 선호를 가진 집단 간에 안정적인 매칭을 찾아내는 알고리즘이다.
이 알고리즘은 1962년 발표된 논문 <대학 입학과 안정적인 결혼>에서 소개한 내용으로, 잠정적 수락 알고리즘(deferrred acceptance algorithm)이라고도 부른다.
이 알고리즘은 다음의 두 가지 내용을 주장한다 :
1. 선호도가 아무리 복잡해도 답은 항상 존재한다.
2. 그리고 그 해를 효율적으로 찾을 수 있다.
커플을 만들어주는 예제에 대해 계속 생각해보자.
N명의 남자와 N명의 여자가 있다. 각각의 사람은 N명의 이성에 대한 선호도를 가지고 있다.
이런 상황에서 안정적인 해를 구하는 방법은 다음의 룰에 따라 모든 커플이 성사될 때까지 '구혼' 라운드를 돌면 된다.
- 남자는 각 라운드에서 선호도가 가장 높은 여자에게 청혼한다.
- 여자는 청혼을 거절하거나, '약혼'을 할 수 있다.
- '약혼'을 했던 여자는 혹시라도 나중에 더 좋은 조건의 청혼이 들어오면 현재의 약혼을 깨고 그를 선택할 수 있다.
이제, 라운드를 돌며 커플을 성사시켜나가보겠다. 쉽게 이해하기 위해 N=4인 경우에 대해 생각해보자
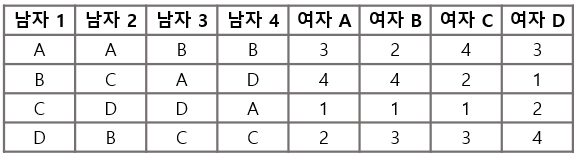
첫 번째 라운드
- 남자는 선호도가 가장 높은 (1순위) 여자에게 청혼한다.
- 청혼을 받은 여자는 1순위가 아니더라도, 일단은 들어온 청혼 중 그나마 선호도가 높은 남성과 약혼을 한다. 어차피 나중에 깰 수 있으니까 안전빵으로 청혼을 받아두는 것이다.
- 그 결과 1, 2로부터 청혼을 받은 여자A는 둘 다 별로지만 그나마 나은 1을 선택하고, 여자 B는 남자 4를 선택한다.
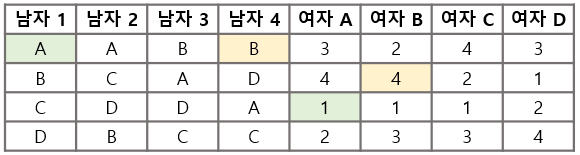
두 번째 라운드
- 솔로인 채 남아 있는 남자3과 4가 재도전을 한다.
- 남자 3은 두 번째로 선호도가 높았던 A에게 청혼을 하는데, 약혼에 있던 A는 가장 선호도 높던 3의 청혼을 받아들이고 1과는 파혼을 한다!!
- 남자 2는 C에게 청혼을 하고, 짝이 없던 C는 2를 받아들인다.
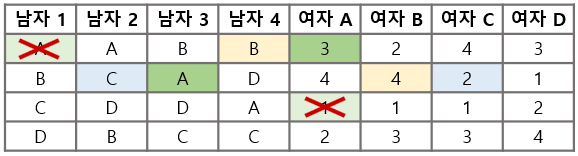
세 번째 라운드
- 솔로가 되어버린 남자 1은 이제 C에게 청혼을 한다. 하지만 2와 약혼해 있는 C는 1보다 2를 좋아하므로 청혼을 거절한다.
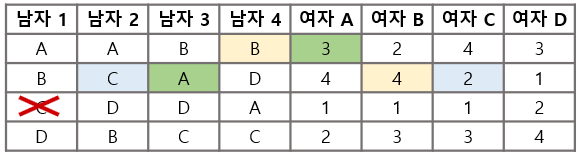
네 번째 라운드
- 마지막으로 남자 1은 D에게 청혼하고, 약혼자가 없던 D는 이를 받아들여 모든 커플이 성사되게 된다.
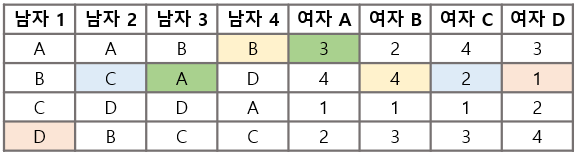
결국 이러한 알고리즘을 돌리게 되면 (1) 모두가 약혼하게 되고, (2) 그 결과는 안정적이다.
(1) 위와 같은 알고리즘은 돌리면, 마지막으로 선호하는 여자에게까지 청혼(최대 NxN번)하게 되면, 더 이상 청혼할 사람이 없어진다. 모든 남자가 약혼을 했거나, 자기 선호도표의 모든 여자에게 청혼을 한 상태가 된다. 이때 약혼이 성사되지 않은 남자는 없는데, 약혼이 성사되지 않은 남자가 있다면 그렇지 않은 여자도 있어야 하는데 이는 모든 여자에게 청혼을 한 상태라는 점에 모순되기 때문이다.
(2) 결과가 안정적이라는 것은 바람피울 상대가 없다는 의미이다. 바람을 피운다는 것은 알고리즘이 끝난 후 두 커플 (m,X), (n,Y)가 있는데, m은 X<Y이고 Y도 n<m인 상태라는 의미인데, 이는 있을 수 없다. m이 생각하기에 X<Y였다면, 이미 그는 먼저 Y에게 청혼한 적이 있다는 것이다. 하지만 맺어지지 않았다는 것은, Y에게 차였거나, 약혼했었더라도 파혼한 상태라는 의미이다. 이는 Y의 랭킹에서 m보다 n이 높다는 의미이므로 이런 상황은 존재할 수 없다.
이 정리는 다양한 상황에서 활용되고 있는데, 재미있는 것은 이 상황에서 남/여의 역할을 바꿀 수도 있고, (여자가 청혼, 남자가 선택) 답이 여러개 있다면 그중 어떤 것을 선택하는 것이 좋은가와 같은 파생 질문들도 생겨날 수 있다.
여기서 재미있는 것은 남자가 먼저 여자에게 청혼하는 알고리즘은 남자에게 유리하다!
이런 선호도표를 상상해보자.
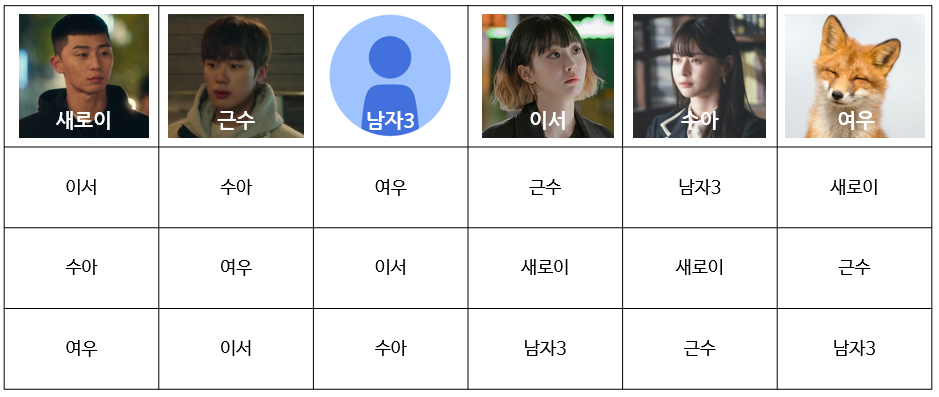
이 상황에서 남자가 먼저 청혼을 하면 청혼을 받은 이서, 수아, 여우는 일단 각각 청혼을 받아들인다. 모든 커플이 성사되었기 때문에 더 이상 라운드가 진행되지 않고, 알고리즘이 종료된다. 남자들은 1순위로 마음에 두고 있던 사람과 맺어져 해피하지만, 여자들은 그렇지가 않다.
반대로 여자가 먼저 청혼을 하게 된다면? 각자 1순위에 두고 있던 근수, 남자3, 새로이에게 청혼을 하게 되고, 그들이 청혼을 받아들여 알고리즘은 종료된다. 여우는 여우 따위 out of 안중이던 새로이와 맺어질 수 있게 된다...! (사심 죄송...)
결국 이 알고리즘에서는 먼저 청혼한 쪽은 연결 가능한 한 사람 중 선호도가 가장 높은 상대와 맺어지게 된다.
그래서 이 알고리즘의 교훈은... "좋아한다면 먼저 고백하라" 라고 한다 ㅋㅋㅋㅋㅋㅋ (by 김민형 교수님)

'Others > Books' 카테고리의 다른 글
| 조직의 성공을 위한 생각의 도구 3가지 (0) | 2020.09.06 |
|---|---|
| 자아 실현을 이룬 인물들의 공통적인 특징 15가지 (1) | 2020.08.30 |
| 모든 순간의 물리학 - 상대성이론, 양자역학, 입자, 공간입자와 루프양자중력 (0) | 2020.08.04 |
| 자율주행 자동차와 도덕적 판단 / 확률론의 선과 악 / 수학이 필요한 순간 : 인간은 얼마나 깊게 생각할 수 있는가 (2) | 2020.02.28 |
| Growth IQ: 성공을 위한 10가지 경로 (2) | 2020.02.22 |