딥러닝 시리즈는 딥러닝 기본 개념을 복습하고, 심화 내용을 스터디하기 위해 시작한 포스팅입니다.
딥러닝을 연구하시는 모두의 피드백과 의견, 소통을 환영합니다 :)
이전 포스팅에서는 딥러닝을 사용해 문제를 풀기 위해 구체화해야 할 세 가지 항목에 대해 이야기했다:
▲ 문제에 대한 출력 ▲ 문제를 풀기 위한 입력 데이터 ▲ 알고리즘의 성능에 대한 수치 척도
2021.04.24 - [AI] - [딥러닝 시리즈] ① 딥러닝으로 풀고자 하는 문제에 대하여
[딥러닝 시리즈] ① 딥러닝으로 풀고자 하는 문제에 대하여
세상에는 수많은 문제들이 있다. 오늘 점심은 무엇을 먹을지부터 시작해서 수도권에 사는 다섯 명의 친구들과 약속 장소를 잡는데 중간 지점을 찾는 문제, 메일을 쓰기가 너무 귀찮은데 키워드
littlefoxdiary.tistory.com

내가 가지고 있는 문제를 잘 정의했다면, 이제 다음의 단계를 통해 모델을 학습해야 한다.
① 학습 데이터 수집
② 적절한 모델 아키텍처 설계
③ 적절한 Loss 함수 설계
④ 적절한 Optimizer을 통해 모델 학습
양질의 데이터를 가능한 한 많이 수집해야 하는 것은 머신러닝에서 자명한 사실이다.
적은 학습 데이터셋으로도 좋은 성능을 내기 위한 연구 분야에 대해서도 추후에 다룰 예정이지만,
기본적으로 좋은 모델은 좋은 학습 데이터에서 나온다.
다음으로는 모델이 입력 데이터로부터 좋은 feature을 추출할 수 있도록 모델 아키텍처를 선택하고,
그를 학습할 수 있는 loss 함수를 정의해야 한다.
이번 포스팅에서는 다양한 문제 상황에서 활용할 수 있는 Loss 함수를 정리한다.

▲ 딥러닝은 학습 데이터를 통해 입력 데이터를 아웃풋으로 매핑하는 방법을 학습하는 과정
회귀분석 - 예측하고자 하는 대상이 실수(real-value)인 문제
Mean Squared Error (MSE) Loss
- 모델 예측값과 실제 값의 차이의 제곱합의 평균으로 정의

Mean Absolute Error (MAE) Loss
- 모델 예측값과 실제 값의 차이의 절대값의 평균으로 정의
- 모델 예측이 크게 빗나간 상황에 대해 MSE에 비해 패널티가 적다.
- 따라서 데이터에 아웃라이어가 적거나 데이터의 아웃라이어를 무시하고 싶을 때 사용

MAE의 경우, Loss가 최저점에 다다랐을 때에도 그라디언트가 크다는 특성이 있다.
이러한 특성은 특히 deep neural network를 사용하는 경우 학습에 있어 좋지 않다.
따라서 딥러닝에서 MAE loss를 사용할 경우,
optimal에 다가갈수록 learning rate를 줄이는 dynamic learning rate scheduling을 적절하게 사용해야 한다.

Mean Squared Logarithmic Error Loss
- 로그 함수로 변환된 실제값과 예측값 사이의 차이 제곱합 사용
- 모델의 타겟 값의 분산이 큰 경우, MSE loss는 큰 error에 대해 크게 패널티를 주는 경우가 있다.
- MSLE loss는 예측값이 큰 경우 예측값과 실제값이 차이가 커지는 것에 대한 패널티를 완화한다.

분류 분석(1) - 인풋을 여러 카테고리 중 하나로 예측하는 문제
(예) 사진을 보고 고양이인지, 강아지인지, 여우인지 분류하기
Negative Log Likelihood Loss (NLL loss)
- 인풋 데이터를 두 개 이상의 클래스 중 하나로 매핑하는 문제에서 사용
- 이 경우 마지막 레이어를 분류하고자하는 카테고리의 개수 C개로 연결하고, 그 아웃풋에 Softmax를 취하는 것이 일반적이다.
- Softmax activation은 아웃풋의 합이 1이 되게 하여, 인풋 데이터가 각각의 클래스에 해당할 확률을 예측하는 효과를 준다.

- 이 softmax activation은 NLL loss와 궁합이 좋다 : NLL loss = L(y)=−log(y)

- NLL loss는 Ground Truth 카테고리에 대해 모델이 예측한 확률값이 작아질수록 <unhappy>한 특성을 가진다.
- 따라서 이 Loss를 최소화하도록 모델을 optimize하면, ground truth에 대한 예측치를 높이는 쪽으로 학습이 이루어진다.
Cross-entropy loss
- 분류 모델을 최적화할 때 보편적으로 사용하는 loss 함수
- 인풋 데이터를 어떤 클래스로 분류한다는 것은, 정답 라벨의 확률을 1, 나머지 라벨의 확률을 0으로 한다는 것으로 볼 수 있다
- 아래 식에서 P(x)는 실제 라벨의 분포, Q(x)는 예측치의 분포를 의미
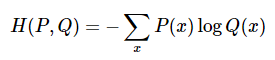

- 모델의 마지막 레이어에 softmax를 취한 후 cross-entropy loss를 계산하게 되면 NLL loss와 수식적으로 같아지기 때문에 softmax cross-entropy loss 등의 이름으로 불리는 것 같음.
분류 분석(2) - 인풋이 속하는 모든 카테고리를 예측하는 문제
(예) 포스터를 보고 영화 장르 예측하기 -> 예측 결과는 {'가족' , '코미디'}와 같이 여러 개의 카테고리에 매핑됨
Binary Cross-entropy loss for each class
- 각각의 클래스에 해당한다 / 아니다를 분류하는 문제로 바꾸어서 접근
- 인풋 라벨은 정답 클래스에 대한 one-hot-encoding 벡터로 넣고, 각각의 카테고리 아웃풋에 대해 binary cross entropy loss를 계산 & 합하여 학습하는 방식
- tensorflow에서는 sigmoid_cross_entropy_with_logits 함수 활용 가능
'AI' 카테고리의 다른 글
| 한국어 언어모델: Korean Pre-trained Language Models (2) | 2021.05.16 |
|---|---|
| [딥러닝 시리즈] ③ Loss 함수 설계하기 (2) (0) | 2021.05.16 |
| [딥러닝 시리즈] ① 딥러닝으로 풀고자 하는 문제에 대하여 (0) | 2021.04.24 |
| 오픈도메인 QA 리서치: Open Domain Question Answering (0) | 2021.03.15 |
| [논문리뷰] DialogBERT: Discourse-Aware Response Generation via Learning to Recover and Rank Utterances (0) | 2021.03.14 |



