MOTIVATION
Transformer 아키텍쳐는 인풋 시퀀스 사이의 attention을 통해 인풋 사이의 관계를 모델링한다.
이때 이 매커니즘만으로는 시퀀스의 순서를 모델링할 수 없다.
예를 들어 "철수 / 가 / 영희 / 를 / 좋아해"라는 시퀀스와 "영희 / 가 / 철수 / 를 / 좋아해"라는 시퀀스에서 "철수"에 해당하는 attention layer의 아웃풋은 두 문장에서 완벽하게 동일하다. 이러한 문제를 해결하기 위해 2017년에 발표된 Transformer 논문에서는 인풋에 위치 인코딩 (position encoding)을 더해주는 방법을 사용하였다.

여기서 위치 인코딩은 (a)sinusoidal 함수를 사용한 결정론적인 벡터나 (b)학습한 벡터를 주로 사용한다.
(a) sinusoidal 함수를 사용한 인코딩
- 인코더나 디코더의 첫 번째 레이어 이전의 인풋에 sinusoid 함수를 사용한 frequency를 더해주는 방법
- 이 방법은 학습 중에 보지 않은 임의의 인풋 길이로 일반화가 가능
(b) 학습된 absolute representation
- 위치 정보 인풋에 대해 projection layer을 학습하여 사용하는 방법
- 학습 중에 보지 않은 더 긴 길이의 인풋으로 확장이 어렵다는 한계가 있다
Self-Attention with Relative Position Representations (2018)
논문 : https://arxiv.org/pdf/1803.02155.pdf
이러한 한계를 극복하고 보다 효율적으로 위치 인코딩을 사용할 수 있도록 < relative position representation >이 제안되었다.
이 relative positional embedding은
1. 기존에 사용하던 absolute embedding을 완벽하게 대체해서 사용할 수 있고
2. 두 인풋 사이의 임의의 관계 (graph 등)에 대해 self-attention을 확장하여 적용할 수 있다.
[3.1] Relation-aware Self-Attention
일반적인 self attention을 수식화하면 아래와 같이 쓸 수 있다.
- 인풋 시퀀스 x = (x1, ..., xn) : 각각 d_x 차원을 가지는 길이 n의 인풋
- 아웃풋 시퀀스 z = (z1, ..., zn) : 각각 d_z 차원을 가지는 길이 n의 아웃풋
아웃풋 시퀀스의 각각의 원소 z_i는 다음과 같은 선형 변환된 인풋 원소의 가중합으로 계산한다 :

여기서 i번째 인풋과 j번째 인풋 사이의 attention score을 의미하는 $\alpha_{ij}$ 는 다음과 같이 계산한다 :

여기서 $e_{ij}$ 는 i번째 인풋과 j번째 인풋을 비교하는 compatibility function을 사용하여 계산한다 :

Transformer(Vaswani et al., 2017)에서는 compatibility function으로 scaled-dot-product를 선택하였다.
▨
본 논문에서는 이 self-attention 매커니즘을 인풋 사이의 pairwise relationship에 대해 일반화한다.
이러한 관점에서, 모델의 인풋이 labeled, directed, fully-connected graph로 표현된 상황을 설정한다.
인풋 원소 x_i와 x_j 사이의 edge(엣지)는 다음과 같은 각각 $d_a$ 차원의 벡터로 표현한다.

이렇게 벡터를 사용해 인풋 사이의 관계를 표현할 수 있는 edge를 학습하는 것은 다음과 같은 특징을 가진다 :
a. attention score을 계산하는 기존의 식을 변형해 별도의 선형 변환 없이도 활용할 수가 있다. (식 (3)&(4))
b. edge representation은 attention head 간에 공유가 가능하고, 이에 따라 저장공간 복잡도를 줄인다.
c. 본 논문에서는 엣지를 표현하는 벡터의 차원(d_a)과 아웃풋 벡터의 차원(d_z)이 같도록 설정했다.
▨
attention layer에서 다음 sub-layer레이어에 전달할 아웃풋을 계산하기 위해 (1) 식을 아래와 같이 수정한다.

=> 아웃풋 representation은 선형 변환된 인풋에 edge 정보를 더한 것의 가중 합으로 계산
=> 다운스트림 인코더/디코더에 있어 각각의 attention head가 선택한 edge type에 대한 정보가 중요할 경우 이 식은 중요함
=> 하지만 기계독해 태스크의 경우 (3)의 식이 크게 중요하지 않은 것으로 밝혀졌다.
인풋 사이의 compatibility를 계산할 때 edge 정보를 반영하도록 (2)식을 아래와 같이 수정한다.

=> i와 j의 attention score을 계산하는 단계에서 i와 j 사이의 관계를 나타내는 edge vector을 더해서 계산
=> (3)과 (4) 식에서 엣지에 대한 정보를 더해주는 것은 이를 프레임워크에서 효율적으로 구현하기 위함
** Relative Position을 표현하는 edge의 예시
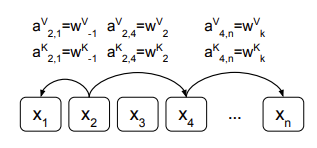
=> 이때 각각의 relative position에 대한 representation은 일정한 거리 k 이내에서 모델이 학습한 벡터
💡기존의 positional encoding은 attention layer에 들어가기 전에 인풋 벡터에 위치 인코딩을 더해주기 때문에, x_i / x_j에 반영되어 있음. Relative Position Encoding은 attention layer에서 수행되는 ▲attention score 계산 ▲아웃풋 벡터 계산 단계에 각각 상대 위치에 대한 representation을 반영해 준 것으로 해석됨.
[3.2] Relative Position Representations
선형적인 시퀀스에 대해 edge는 인풋 인자들 사이의 상대적인 위치 차이에 대한 정보를 담을 수 있다.
이때 상대 위치에 대한 최대값은 k라는 값으로 지정해 clipping한다.
=> 이는 상대적인 위치에 대한 정확한 값은 특정 거리 이상에서는 중요하지 않다는 가정에 기반함
=> 최대 거리를 clipping하게 되면, 학습 중에 보지 못한 길이로 일반화가 가능하다는 장점
상대 위치를 고려하는 최대 값을 k로 설정하면, 2k + 1개의 구별되는 edge label을 고려하게 된다.

이러한 reletive position representation은 학습을 통해 배운다.
T5 Relative Position Encoding
2020년 구글에서 발표한 언어 모델 논문인 T5에서는 relative position encoding을 활용한다.
두 인풋 사이의 상대적인 거리를 고려한다는 기본 전제는 같지만, T5에서 사용한 방식은 제안된 방법과 조금 다르다.
Relative position embedding은 self-attention의 key와 query 사이의 거리에 따라 학습된 embedding을 생성한다.
T5에서는 position embedding으로 단순하게 scalar을 사용한다.
그리고 이 스칼라는 attention weight를 계산할 때 logit에 더해주는 값으로 사용한다.
뿐만 아니라 효율성을 위해 position embedding 값은 모든 레이어에서 공유하되,
각 레이어의 attention head에서는 각기 다른 학습된 position embedding을 사용한다.
즉, 가능한 key-query 거리의 범위에 따라 고정된 개수의 embedding이 학습되게 된다.
T5에서는 32개의 임베딩을 사용하였고, 거리에 따라 그 범위가 로그적으로 증가하도록 설정하였다.
128이 넘는 거리에 대해서는 같은 position embedding을 부과하게 된다.
Pytorch Implementation
huggingface transformer 깃허브를 보면 relative position encoding이 어떤 식으로 작동하는지 볼 수 있다.
GitHub - huggingface/transformers: 🤗 Transformers: State-of-the-art Machine Learning for Pytorch, TensorFlow, and JAX.
🤗 Transformers: State-of-the-art Machine Learning for Pytorch, TensorFlow, and JAX. - GitHub - huggingface/transformers: 🤗 Transformers: State-of-the-art Machine Learning for Pytorch, TensorFlow, a...
github.com
import math
import torch
def _relative_position_bucket(relative_position, bidirectional=True, num_buckets=32, max_distance=128):
relative_buckets = 0
if bidirectional:
num_buckets //= 2
relative_buckets += (relative_position > 0).to(torch.long) * num_buckets
relative_position = torch.abs(relative_position)
else:
relative_position = -torch.min(relative_position, torch.zeros_like(relative_position))
# now relative_position is in the range [0, inf)
# half of the buckets are for exact increments in positions
max_exact = num_buckets // 2
is_small = relative_position < max_exact
# The other half of the buckets are for logarithmically bigger bins in positions up to max_distance
relative_postion_if_large = max_exact + (
torch.log(relative_position.float() / max_exact)
/ math.log(max_distance / max_exact)
* (num_buckets - max_exact)
).to(torch.long)
relative_postion_if_large = torch.min(
relative_postion_if_large, torch.full_like(relative_postion_if_large, num_buckets - 1)
)
relative_buckets += torch.where(is_small, relative_position, relative_postion_if_large)
return relative_buckets
인풋 시퀀스 512인 문장에 대해 Self-attention 상황을 가정하면, relative position은 다음과 같이 구할 수 있다.
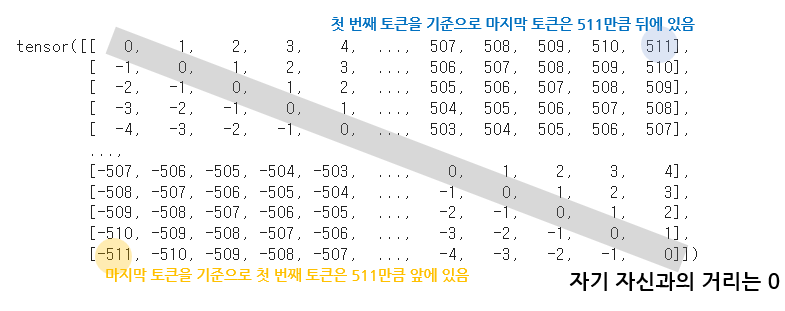
이제 이 relative position을 _relative_position_bucket에 대입하면 상대적인 거리에 따른 버킷 값을 얻을 수 있다.

이 버킷 값은 scalar로 임베딩 하여 attention score을 구할 때 logit에 더해져 위치 정보를 반영하게 된다.
(추정 건데, 가까운 거리에 있는 토큰이 더 큰 가중치를 받을 수 있게 학습되지 않을까?)

'AI' 카테고리의 다른 글
| [논문리뷰] 알파코드 - Competition-Level Code Generation with AlphaCode (0) | 2022.03.30 |
|---|---|
| [ML Ops] - 지속가능한 AI서비스를 위한 Model Drift의 인지 및 관리 (0) | 2022.02.20 |
| [논문리뷰] Multimodal Neurons in Artificial Neural Networks (2) | 2021.11.21 |
| Topic Segmentation 서베이 (2) | 유사도 기반의 클러스트링 - Dot Plotting (0) | 2021.10.10 |
| Topic Segmentation 서베이 (1) | Lexical Similarity 기반 기법 - TextTiling in Python (0) | 2021.10.05 |



