원문 - http://www.eecs.qmul.ac.uk/~mpurver/papers/purver11slu.pdf
본 서베이에서는 긴 컨텍스트를 주제적 일관성이 있는 segment로 나누는 방법에 대해 다룹니다.
포스팅은 이 중에서 대화 전사 텍스트 혹은 대화 STT 결과물 등을 segment하는 방법에 초점을 맞추어 정리하였습니다.
지난 글 :
2021.10.05 - [AI] - Topic Segmentation 서베이 (1) | Lexical Similarity 기반 기법 - TextTiling in Python
Topic Segmentation 서베이 (1) | Lexical Similarity 기반 기법 - TextTiling in Python
원문 - http://www.eecs.qmul.ac.uk/~mpurver/papers/purver11slu.pdf 본 서베이에서는 긴 컨텍스트를 주제적 일관성이 있는 segment로 나누는 방법에 대해 다룹니다. 포스팅은 이 중에서 대화 전사 텍스트 혹은..
littlefoxdiary.tistory.com
-> Speech Segmentation 아이디어 / TextTiling / Latent Concept Modeling
방법론 2. 유사도 기반의 클러스터링
이전 포스팅에서는 일관성이 떨어지는 부분, 즉 토픽의 경계선을 찾는 데에 초점을 맞추었다.
하지만 다른 접근법으로 일관성이 높은 토픽 세그먼트를 찾아가는 방법도 가능하다.
즉, 이웃한 부분에 대해 비슷한 부분을 묶어 가다 보면 발화문에 대한 segmentation을 얻을 수 있다.
이때 유사도가 가장 높은 피크로부터 클러스터링을 진행하는 agglomerative clustering을 사용할 수도 있지만,
divisive clustering 기법이 보다 잘 작동하는 것으로 밝혀졌다.
💡 Dot-Plotting ( Reynar 1994 )
문서를 각각의 발화문 내의 단어에 대한 2차원의 매트릭스로 표현한다. (등장하는 순서대로 나열)
이후 매칭되는 단어가 있는 부분에 대해서는 점을 찍는다.
이렇게 하면 대각선 부분은 항상 매칭되는 단어가 있으므로 0이 아닌 것으로 표현이 된다.
또한, 토픽에 따라서 비슷한 주제가 자주 등장하는 발화문 근처에는 사각형의 영역이 표현된다.
이제 이러한 사각형의 경계선을 토픽의 경계선으로 표시할 수 있다.
사각형 내의 점의 밀도를 극대화하고, 경계선 밖에 있는 사각형의 점의 밀도를 극소화하는 경계선을 찾는 것이다.
이 방법은 학습 데이터 없이 비지도학습 기반으로 수행할 수 있다.
대신 경계선 탐색을 끝내기 위한 기준점 등을 하이퍼파라미터로 설정해야 한다.
Reynar은 best-first 탐색 기법을 사용하여 경계선 바깥의 density를 최소화하였고, 경계선의 개수는 알려져 있다고 가정했다.

이 방법은 Choi(2000)에서 개선되었는데, 단어 자체가 아니라 문장 단위로 이 알고리즘을 수행하였고, 코사인 유사도 기반의 매트릭을 사용하였으며 finishing 알고리즘으로 gradient criterion을 적용하였다.
여기에서도 Latent concept modeling 방법을 적용할 수 있다 (Choi et al. 2001)
Latent semantic analysis 기반의 방법을 사용하면 정확도를 향상시킬 수 있지만, Popescu-Belis et al. (2005)의 연구에 따르면 이 기법의 성능 향상 기여도는 회의 데이터에 대해서는 적은 것으로 밝혀졌다.
이 방법들은 원래부터 구별이 가능한 텍스트 문서에 대해 진행되었기 때문에, 대화 데이터에 대해서는 구분점이 명확하지 않다는 한계가 있다. 대화에서는 주제의 전환이 급격하기보다는 부드럽게 진행되기 때문이다.
하지만 Malioutov and Barzilay (2006) 연구에 따르면
Δ 알고리즘을 exact solution을 찾을 수 있도록 수정하고
Δ 적합한 유사도 매트릭을 적용하며
Δ 유사도를 계산할 때 long-range distance를 제한하는 방법을 통해 대화 도메인에도 이 방법을 적용할 수 있었다.
💡 Minimum cut model for spoken lecture segmentation
- Source (1) : https://dspace.mit.edu/handle/1721.1/51651
- Source (2) : https://aclanthology.org/P06-1004.pdf
Topic segmentation 문제를 graph-partitioning task로 인식하여 커팅 기준을 최적화하는 기법을 도입한다.
텍스트를 weighted undirected graph로 추출하는데, 그래프의 노드는 문장이고 엣지 가중치는 pairwise sentence similarity를 나타낸다. 이제 텍스트 segmentation 문제는 normalized-cut criterion을 최적화하는 그래프 partitioning 문제로 인식할 수 있다. 이 방법은 기존 연구와 달리 세그먼트 내의 유사성을 단순히 단어 간의 유사도만으로 결정하는 것이 아니라, 텍스트 내의 다른 세그먼트에 있는 단어와의 연관성도 고려한다는 점이다.
Step 1. Text Processing
그래프를 생성하기 전에 단어에 대한 원형 복원(stemming)을 진행하여 단어 빈도에 대한 sparsity를 완화한다.
너무 자주 등장하는 한정사(determiner)나 인칭대명사(personal pronoun)는 세그먼트 사이의 유사도를 찾는 데에 방해가 되므로 stopword 로 지정하여 제거한다.
Step 2. 그래프 생성
Normalized cut criterion은 노드들 사이의 lont-term 유사도 기반의 관계를 고려한다. 이 효과를 위해서는 모든 노드의 연결을 고려하는 fully-connected graph를 생성해야 하지만, 긴 텍스트에 대해 모든 발화문과의 관계를 고려하는 것은 오히려 segmentation accuracy를 떨어뜨릴 수 있다. 따라서, 특정 거리 threshold를 넘는 문장들 간의 엣지는 고려하지 않는다. 이렇게 그래프 크기를 줄이는 것은 계산적으로도 비용을 줄일 수 있다.
그래프의 노드로는 문장을 사용할 수도 있지만, 겹치지 않는 고정된 길이의 단어 블록을 사용할 수도 있다. 예를 들어 강의 전사록 같은 경우 문장의 바운더리가 명확하지 않고, 짧은 발화문의 경우 코사인 유사도 점수에 skew 를 야기할 수 있기 때문에 단어 블록을 사용하는 것이 좋다.
Step 3. 유사도 계산
유사도을 위해 문장은 단어 빈도에 대한 벡터로 나타내고, 목적은 의미적으로 비슷한 문장을 찾아내는 것으로 한다.
이를 위해서는 의미적으로 현저하게 유사한 단어는 계산에 있어 큰 가중치를 주어야 한다.
특히 일반적인 대화에서는 잘 나오지 않는 단어이지만, Topic segmentation을 수행하려는 문서의 도메인에서는 중요한 단어들을 신경써야 한다. 예를 들어 강의 내용이 SVM 알고리즘에 대한 것이라고 가정하자. 일반적인 문서에서라면 "SVM"이라는 단어는 드문 단어이기 때문에 많은 정보를 포함하지만, 이 강의에서는 하위 주제의 분포에 대해서 그다지 많은 정보를 주지 않을 것이다. 즉, 같은 단어라도 유사도 계산에 있어 문서에 따라 각기 다른 가중치를 가진다.
이런 문제를 해결하기 위해 Information Retrieval에서 자주 사용하는 TF-IDF 점수를 약간 변형하여 사용한다.
논문에서는 강의에 대한 전사 스크립트를 실험용 문서로 사용한다. 여기서 전사 스크립트는 유니폼하게 N개의 부분으로 쪼갠 후 각각의 조각을 TF-IDF 계산에서 문서와 같이 취급한다.
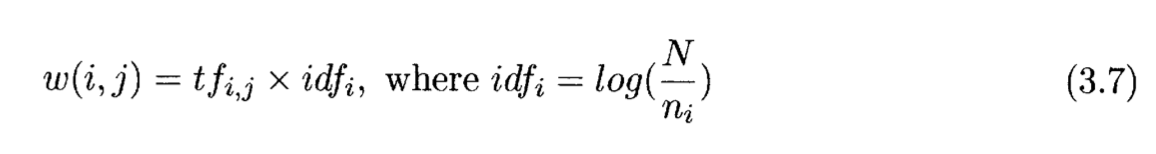
위 식에서 n_i는 단어 i가 등장하는 문서 조각(chunk)의 개수이고, idf_i는 단어 i가 문서에서 등장하는 inverse segment frequency를 나타낸다. tf_i,j는 j번째 문서 조각에 등장하는 단어 i의 빈도수이다. 즉, 단어에 대한 가중치는 각각의 전사 스크립트별로 다르게 계산되는 것이다. (각 강의에 따라 토픽과 단어의 분포가 다르기 때문)
어휘에 대한 가중치를 계산한 후에는 각각의 문장 쌍에 대해 tf-idf가중치로 가중치가 주어진 단어 빈도수에 대해 코사인 유사도 점수를 계산한다.

위 식에서 f_x,j는 문장 x에서 단어 j의 빈도, w_x는 문장 x에 대한 웨이트 벡터, cid(x)는 단어를 포함하는 문장에 대한 인덱스이다. (word chunk index containing the sentence.)
마지막으로 실제 엣지 가중치는 코사인 유사도의 exponential값을 사용하여 단어적 유사도가 낮은 쌍과 높은 쌍의 차이를 극대화한다.

Step 4. Smoothing
그래프에서 각 노드를 연결하는 엣지의 웨이트를 나타내는 유사도 행렬은 유사도 정보를 문장 단위에서 모델링한다. 같은 토픽의 문장들 간의 유사도는 다른 토픽에 속한 문장과의 유사도보다 평균적으로 높겠지만, 개별 점수로 볼 때는 분산이 클 것이다. 따라서 유사도 점수를 스무딩하여 사용한다.
> Exponentially Weighted Moving Average (EWMA)
근접한 문장에서 등장하는 단어에 대한 카운트를 현재 문장 feature vector에 더하는 기법.
이때 단어의 카운트는 해당 문장이 현재 문장과 얼마나 떨어져 있는지에 따라 가중치를 가지게 된다.
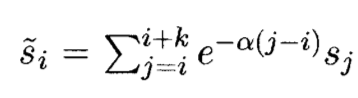
이러한 스무딩을 적용하게 되면 두 문장 사이의 유사도를 계산할 때에 주변에 있는 문장과의 유사도를 고려할 수 있다.
실험적으로 수행해 보았을 때, 이웃문장 중 이전에 등장했던 단어들만을 고려하여 계산하는 것이 성능이 더 좋았다.
Step 5. Cutoff
이제, 구성한 그래프 G = {V, E} 를 두 개의 노드의 집합 A, B로 나누는 문제를 생각해 보자.
여기서 목표는 두개의 집합을 연결하는 엣지의 합으로 정의하는 cut 을 최소화하도록 그래프를 분리해야 한다.
즉, 가장 유사하지 않은 두 집단 A, B를 선택해 문장을 나눔으로서 다음을 최소화하는 것을 목표로 한다 :

하지만 동시에 두 파티션이 서로 최대한 다를 뿐만 아니라, 각 집단 내에서는 노드간의 유사도가 높음으로써 동질성이 있어야 한다. 이 두 가지 조건을 충족하기 위해 normalized cuts를 성의하는데, cut value는 각 파티션의 볼륨에 따라 정규화된다. 파티션의 볼륨은 전체 그래프에서 해당 파티션의 엣지들의 합으로 정의한다 :
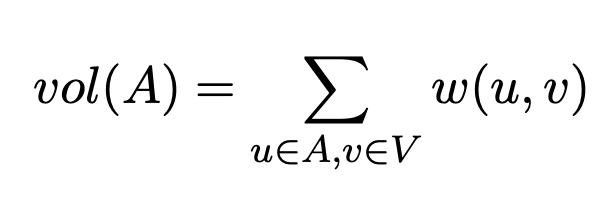
이제 normalized cut은 다음과 같이 정의할 수 있다 :
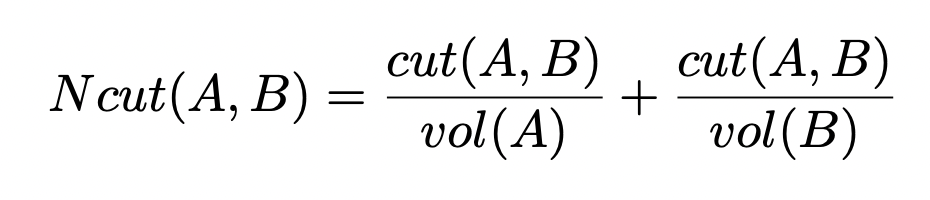
이 목적함수를 최소화하는 것은 파티션간의 유사도는 최소화하면서, 파티션 내의 유사도는 극대화할 수 있도록 한다.
또한 이 함수는 k개로 파티셔닝을 진행하는 것으로도 확장할 수 있다 :
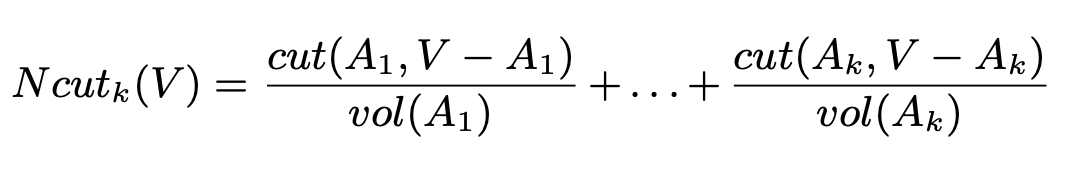
Normalized cut을 최소화하는 문제는 NP-complete문제이다. 하지만 여기서는 segmentation이 선형적이라는 제약조건이 있기 때문에, 이 문제를 다이내믹 프로그래밍을 통해 풀 수 있다 :





